Korrelaatio ja riippuvuusluvut

  Korrelaatio
     Pearsonin korrelaatiokerroin
  Riippuvuusluvut
     Luokitteluasteikollisille muuttujille
        Kontingenssikerroin
        Yulen Q
        Phi kerroin
        Riski
        Cramerin V
        Lambda
        Epävarmuuskerroin
     Järjestysasteikollisille muuttujille
        Parien käsite
        Spearmanin rho
        Kendallin tau-b ja tau-c
        Goodmanin ja Kruskalin gamma
  Osittaiskorrelaatio
  Harjoituksia

Korrelaatio

Kahden muuttujan välisen riippuvuuden astetta voidaan nimittää yleisessä merkityksessä korrelaatioksi. Jos korrelaatio on voimakasta, voidaan toisen muuttujan arvoista päätellä toisen muuttujan arvot melko täsmällisesti. Jos korrelaatio on heikko, ei muuttujien välillä ole yhteisvaihtelua. Korrelaatiolla voidaan joskus viitata myös tavallisimmin käytettyyn Pearsonin tulomomenttikorrelaatioon, jota selvitetään seuraavassa. Tämä riippuvuuslukuja koskeva tietovarannon osuus esittelee erilaiset tunnusluvut hyvin tiiviisti keskittyen kuvaamaan esimerkein niiden laskentaperiaatteita.

Pearsonin korrelaatiokerroin, r

Yleisin käytetty korrelaatiota kuvaava tunnusluku on Pearsonin tulomomenttikorrelaatiokerroin (r). Se on vähintään kahden intervalliasteikollisen muuttujan keskinäisen lineaarisen riippuvuuden voimakkuutta kuvaava tilastollinen tunnusluku. Korrelaatiokerroin lasketaan kaavalla

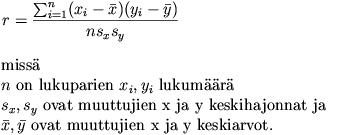
Tulomomenttikorrelaatiokertoimen arvo vaihtelee välillä -1 ... +1. Korrelaatiokertoimen ollessa 0, ei muuttujien välillä ole lineaarista riippuvuutta. Vastaavasti arvoilla (+/-) 1 muuttujien välillä on täydellinen positiivinen / negatiivinen lineaarinen riippuvuus. Täydellisen lineaarisen riippuvuuden tapauksessa muuttujien kaikki arvot sijoittuvat hajontakuviossa samalle suoralle viivalle. Yleensä muuttujien välinen korrelaatiokerroin poikkeaa nollasta. Tämä voi johtua myös sattumasta. Korrelaatiokertoimen merkitsevyystason avulla voidaan arvioida kertoimen tilastollista merkitsevyyttä. Usein raportoidaan myös Pearsonin korrelaatiokertoimen neliö (r²). Esimerkiksi jos r² = 0.32 sanotaan, että selittävä muuttuja selittää 32 % selitettävän muuttujan varianssista.

Myös korrelaatiokertoimen käyttöön liittyy useita yleisiä tilastoanalyysin sudenkuoppia:

• Korrelaatiokerroin ei automaattisesti anna informaatiota siitä vallitseeko, muuttujien välillä kausaalinen suhde.
• Jos myös muut muuttujat kuin selittävä muuttuja vaikuttavat tarkasteltavaan muuttujaan, silloin kaikki yhteinen kovarianssi, jota niillä on selittävän muuttujan kanssa, luetaan ainoalle selittävälle muuttujalle.
• Jos muuttujien välillä on epälineaarista riippuvuutta, sen määrä tulee huomattavasti aliarvioiduksi.
• Yksittäiset poikkeavat havaintoarvot voivat vaikuttaa suuresti korrelaatiokertoimen arvoon, minkä vuoksi on suositeltavaa aina tulostaa tutkittavien muuttujien hajontakuvio.
• Korrelaatiokerroin voi olla harhaanjohtava, esimerkiksi silloin, jos tarkasteltavat muuttujat eivät ole homoskedastisia.

 

Riippuvuusluvut

Riippuvuusluvut luokitteluasteikollisille muuttujille

Kontingenssikerroin (Contingency Coefficient)

Kontingenssikerroin C kuvaa kahden luokitteluasteikollisen muuttujan välistä riippuvuutta ja sen määrittelee kaava:

:n testisuureen arvon laskeminen ("khii toiseen testi") on selitetty ristiintaulukoinnin yhteydessä. Korrelaatiokertoimen arvot vaihtelevat välillä 0 ... 1. Kontingenssikertoimen tilastollista merkitsevyyttä testataan -testisuureen avulla, joka on -jakautunut vapausastein (l - 1)(m - 1), jossa l ja m ovat muuttujien luokkien lukumäärät.

Tarkastellaan sitten esimerkkiä, jossa tutkitaan kahden luokitteluasteikollisen muuttujan Y (vastaajan asuinmaakunta) ja X (vastaajan äidinkieli) riippuvuutta henkilöaineistossa. Näiden muuttujien kaksiulotteinen yhteisfrekvenssijakauma on seuraava:

	äidinkieli (X)
asuinmaakunta (Y)		suomi	ruotsi
	Uusimaa	(a) 76	(b) 13
	muu maakunta	(c) 229	(d) 5

Taulukon perusteella arvoksi saadaan 19.053, joten kontingenssikertoimeksi saadaan (sijoittamalla edellä esitettyyn kaavaan):

Asuinmaakunnalla ja äidinkielellä olisi siis verrattain pieni riippuvuus.

Kontingenssikertoimen käyttökelpoisuus empiirisenä riippuvuuslukuna perustuu ensisijaisesti siihen, että muuttujilta ei vaadita kuin luokitteluasteikollinen mittaustarkkuus. Myöskään jakaumaoletuksia ei ole. Kontingenssikertoimella on muutamia heikkouksia:

• Kontingenssikerroin ei voi saada negatiivisia arvoja, joten sen avulla ei voi päätellä riippuvuuden suuntaa.
• Kontingenssikertoimien keskinäinen vertailu ei ole mielekästä, mikäli ne perustuvat erikokoisiin taulukoihin.
• Suurin arvo, jonka kontingenssikerroin voi saavuttaa, on aina pienempi kuin 1.
  Lisäksi taulukoille, joiden rivi- ja sarakemäärät ovat yhtä suuret, suurin arvo on sqrt((r-1)/r). Esimerkiksi taulukolle, jossa on kaksi saraketta ja riviä suurin saavutettavissa oleva kontingenssikertoimen arvo on siis sqrt((2 - 1)/2) = 0.71.
• Kontingenssikerroin ei ole vertailukelpoinen järjestyskorrelaatiokertoimien eikä Pearsonin korrelaatiokertoimen kanssa.

Yulen Q

Käytetään kahden luokitteluasteikollisen dikotomisen muuttujan riippuvuuden tarkastelussa. Yulen Q määritellään 2x2 yhteisfrekvenssijakaumataulukon diagonaalisolujen tulojen erotuksen ja summan osamääränä. Siis:

 

Esimerkkitaulukon tapauksessa Q:n arvoksi saadaan:

 

Phi kerroin,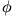

Tätäkin kerrointa käytetään kahden luokitteluasteikollisen dikotomisen muuttujan riippuvuuden tarkastelussa. Jakaumaoletuksena vaaditaan, että muuttujat olisivat luonnollisesti dikotomisia. Phi -kerroin lasketaan kaavalla:

 

Esimerkkitaulukon tapauksessa Phi:n arvoksi saadaan:

 

Tuloksesta huomataan, että tarkasteltavien muuttujien riippuvuus on suunnilleen samaa luokkaa kuin kontingenssikertoimella laskettuna. Lisäksi saadaan selville riippuvuuden suunta, joka on negatiivinen.

Riski (Relative Risk, RR)

Tämä suhdeluku sopii niin ikään kahden luokitteluasteikollisen dikotomisen muuttujan riippuvuuden tarkasteluun. Tunnusluku on yleinen terveystieteissä, mutta sopii myös sosiaalitieteiden tilanteisiin, joissa toinen muuttuja on käsittely/syy ja toinen vaikutus/seuraus. Riski ja ristitulosuhde (odds ratio) lasketaan kaavoilla:

 

 

Cramerin V

Cramerin V on suosittu -perustainen riippuvuusluku, jota käytetään kahden luokitteluasteikollisen muuttujan riippuvuuden tarkastelussa. Se lasketaan kaavalla:

V vaihtelee välillä 0 ... 1, riippumatta yhteisjakaumataulukon koosta. Koska V:n otosjakauma tunnetaan, sen keskivirhe ja merkitsevyys voidaan laskea. Esimerkkitaulukossa sen arvoksi saadaan:

 

Lambda

Lambdaa käytetään kahden luokitteluasteikollisen muuttujan riippuvuuden tarkastelussa ja sen symmetrinen arvo lasketaan kaavalla:

Lambda vaihtelee välillä 0 ... 1. Se kertoo, kuinka tarkasti voidaan ennustaa toisen muuttujan arvo, kun toisen muuttujan arvo tiedetään. Koska lambdalla on tunnettu otosjakauma, voidaan sen keskivirhe ja merkitsevyys laskea. Tilastolliset ohjelmistot, kuten esimerkiksi SPSS, laskevat asymptoottisen keskivirheen (ASE, Asymptotic Standart Error).

Esimerkkitaulukossa lambdan arvoksi saadaan:

 

Lambdasta on myös asymmetrinen versio, jossa täytyy määritellä kumpi muuttuja on selittäjä ja kumpi selitettävä. Kaavaksi muodostuu tällöin:

Jos halutaan selittää asuinmaakuntaa (selitettävä) äidinkielellä (selittäjä), tulokseksi saadaan:

 

Epävarmuuskerroin (Uncertainty, Entropy Coefficient)

Epävarmuuskerroin on lambdaa vastaava tunnusluku, joka vaihtelee välillä 0 ... 1. Sen keskivirhe ja merkitsevyys voidaan laskea. Tulkintana on, lambdaa vastaavasti, ennuste toisen muuttujan arvosta, jos tiedetään toisen muuttujan arvo. Epävarmuuskerroin on asymmetrinen riippuvuusluku. Kertoimen arvo riippuu siis siitä, kumpi muuttuja on selittävä/selitettävä. Useat tilastolliset ohjelmistot laskevat myös symmetrisen epävarmuuskertoimen, joka on keskiarvo kahdesta asymmetrisestä kertoimesta. Merkinnässä UC(R|C) rivimuuttuja (Y) on selitettävä ja sarakemuuttuja (X) selittäjä.

 

Riippuvuusluvut järjestysasteikollisille muuttujille

Tarkastellaan kahta järjestysasteikollista muuttujaa X (vastaajan koulutus) ja Y (vastaajan bruttotulot/kk) henkilöaineistossa. Näiden muuttujien kaksiulotteinen yhteisfrekvenssijakauma on seuraava:

	bruttotulot/kk (X)
koulutus (Y)		alle 1800 €	1800-2300 €	yli 2300 €
	perusaste	(a) 33	(b) 25	(c) 3
	väh. keskiaste	(d) 54	(e) 102	(f) 56

Parien käsite

Ylläolevan taulukon perusteella voidaan määritellä:

Parin tyyppi	Parien lukumäärä	Symboli
samansuuntainen	a(e+f) + b(f)	P
vastakkaissuuntainen	c(d+e) + b(d)	Q
sidos muuttujassa X	ad + be + cf	Xo
sidos muuttujassa Y	a(b+c) + bc + d(e+f) + ef	Yo

Spearmanin rho,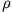

Spearmanin on useimmin käytetty järjestyskorrelaatiokerroin vähintään järjestysasteikollisten muuttujien välillä. Kertoimen laskenta aloitetaan järjestämällä aineisto suuruusjärjestykseen toisen muuttujan suhteen. Tämän jälkeen annetaan muuttujille järjestysluvut (rank) (1, 2, ..., N) muuttujan arvojen mukaan ja lasketaan havaintopareittain järjestyslukujen erotus D . Itse kerroin saadaan tällöin kaavasta:

 

Voidaan osoittaa, että Spearmanin on järjestysluvuista laskettu Pearsonin korrelaatiokerroin. Laskettaessa :ta edellytetään, että muuttujien järjestysluvuissa ei esiinny tasatuloksia eli sidoksia. Pieni sidosmäärä voidaan käsitellä käyttämällä tasatuloksista järjestyslukujen keskiarvoja. Esimerkkiaineistolla :n arvoksi tulee 0.345.

Kendallin tau-b ja tau-c

Kendallin tau-b on riippuvuusluku, jonka laskenta perustuu saman- ja vastakkaissuuntaisten parien erotukseen jaettuna X- ja Y-muuttujien ei sidottujen parien lukumäärien geometrisellä keskiarvolla eli:

 

Tau-b:tä käytetään usein 2x2 jakaumataulun tilanteessa, mutta se sopii myös useampiluokkaisiin muuttujiin. Useampiluokkaisille muuttujille on kehitetty variaationa tau-c, joka lasketaan kaavalla

 

Goodmanin ja Kruskalin gamma,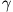

Gamma on symmetrinen riippuvuusluku, joka vaihtelee välillä -1 ... +1. Se perustuu saman- ja vastakkaissuuntaisten parien väliseen eroon, joka lasketaan kaavalla

 

Koska gammalla on tunnettu otosjakauma, joka lähenee suurilla otoksilla normaalijakaumaa, voidaan sen keskivirhe ja merkitsevyys laskea.

Osittaiskorrelaatio

Osittaiskorrelaatio on kahden muuttujan välinen korrelaatio, kun yhden tai useamman muuttujan vaikutus on poistettu (vakioitu). Tämä voidaan tehdä myös laskemalla muuttujien korrelaatio kolmannen tekijän osajoukoissa. Esimerkiksi jäätelön kulutus ja hukkumiskuolemien määrä korreloivat voimakkaasti. Muuttujien välinen korrelaatio johtuu siitä, että molemmat korreloivat lämpötilan kanssa. Sisällöllisesti mielekäs korrelaatio saadaan laskemalla osittaiskorrelaatio jäätelön kulutuksen ja hukkumiskuolemien määrän välillä, kun lämpötilan vaikutus on poistettu. Osittaiskorrelaatiosta ei kuitenkaan näy, onko alkuperäinen kahden muuttujan yhteys samanlainen vai erilainen vakioitavan muuttujan eri arvoilla. Tulkinnan kannalta on tärkeää tietää muuttujien aikajärjestys. Osittaiskorrelaatiota merkitään usein luvulla r_xy.z niin, että vakioitava muuttuja erotetaan pisteellä alkuperäisen korrelaation muuttujista. Laskentakaava osoittaiskorrelaatiolle on:

 

Myös osittaiskorrelaatio kuvaa muuttujien lineaarista yhteyttä, joka vaihtelee välillä -1 ... +1. Osittaiskorrelaatio voidaan yleistää useamman muuttujan samanaikaiseen vakiointiin lisäämällä vakioitavia muuttujia ja soveltamalla kaavaa useita kertoja.

Harjoituksia

1. Kaksi professoria asettaa tutkijan virkaan hakijat seuraavaan paremmuusjärjestykseen.

Määritä Spearmanin rho. Ovatko professorien mielipiteet samansuuntaiset?

2. Laske Pearsonin korrelaatiokerroin oheisesta aineistosta. Jos aineistoon lisätään havainto (20,100), niin miten korrelaatiokerroin muuttuu?