KvantiMOTV on päivitetty Kvantitatiivisen tutkimuksen verkkokäsikirjaksi. Lue uusi artikkeli Regressioanalyysin oletukset ja Regressiomallin arviointi.
Regressioanalyysin rajoitteet
Regressioanalyysi on joustavuudessaan erinomainen menetelmä muuttujien riippuvuussuhteiden tarkasteluun. Siihen liittyy kuitenkin rajoitteita, joista menetelmän käyttäjän on hyvä olla tietoinen. Tässä yhteydessä rajoitteet esitellään vain lyhyesti. Regressioanalyysi tarjoaa myös monia mahdollisia tapoja ottaa rajoitteet huomioon ja "korjata" niiden vaikutukset regressioanalyysissa. Lisätiedot osuudessa listataan useita kirjoja, joista saa tarkempia tietoja näistä mahdollisuuksista.
a) Lineaarisuusoletus. Regressioanalyysin avulla voidaan tutkia muuttujien välisiä lineaarisia eli suoraviivaisia kausaalisuhteita. Jos regressioanalyysin tulokset osoittavat, että selittävällä muuttujalla ei ole tilastollisesti merkitsevää yhteyttä selitettävään muuttujaan, tarkoittaa tämä tarkasti ottaen ainoastaan sitä, ettei lineaarista yhteyttä esiinny. Muuttujilla voi kuitenkin olla epälineaarinen yhteys. Kuviossa 2 on esitetty kaksi tilannetta, joissa x- ja y-muuttujien välillä on epälineaarinen yhteys.
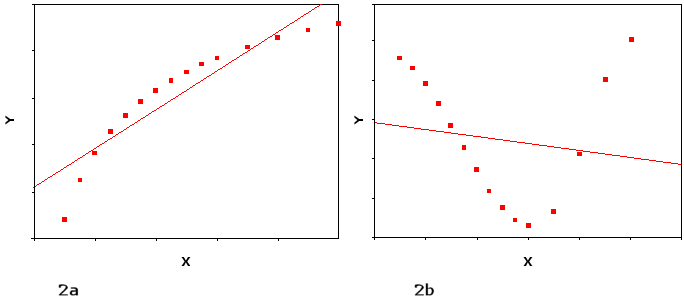
Kuvio 2. Esimerkkejä muuttujien epälineaarisista yhteyksistä.
Kuvion 2 kummassakin esimerkissä pisteet tarkoittavat muuttujien havaittuja arvoja ja suora on niiden pohjalta piirretty regressiosuora. Kuvion 2a tilanteessa x- ja y-muuttujien yhteys on epälineaarinen, mutta poikkeama lineaarisuudesta ei ole suuri. Tässä tilanteessa muuttujan x regressiokerroin olisi positiivinen ja se antaisi kohtuullisen hyvän likiarvon muuttujien välisestä suhteesta.
Esimerkki kuviossa 2b kuvaa tilannetta, jossa x- ja y-muuttujan suhde on erittäin epälineaarinen. Regressiosuora on lähes vaakasuora (eli regressiokerroin on lähellä nollaa), mikä ilmaisee sen, että muuttujilla ei ole lineaarista yhteyttä toisiinsa. Jos tutkija tällaisen analyysin pohjalta toteaa, että x-muuttujan avulla ei voida selittää y-muuttujan arvoja, tekee hän kuitenkin virheen, koska muuttujilla on selkeä epälineaarinen yhteys toisiinsa.
Regressioanalyysin avulla voi kuitenkin tarkastella myös muuttujien epälineaarisia suhteita. Tämä tapahtuu muuttujien muunnosten avulla. Muunnoksen kohteena voi olla sekä selitettävä tai selittävät muuttujat tilanteen mukaan. Lievien epälineaarisuuksien korjaamiseen käytetään logaritmi- tai neliöjuurimuunnosta. Jos kuvion esimerkissä 2a x-muuttujasta otetaan luonnollinen logaritmi ja tämä uusi muuttuja sisällytetään regressioanalyysiin alkuperäisen x-muuttujan sijasta, paranee mallin selitysosuus huomattavasti. Tämä johtuu siitä, että y-muuttujalla ja uudella selittävällä muuttujalla (x:n logaritmi) on lähes täydellinen lineaarinen riippuvuus toisistaan.
Esimerkissä 2b epälineaarisuus on niin vahva, että yksinkertaisilla muuttujamuunnoksilla siitä ei selvitä. Muuttujien välinen yhteys on kuitenkin sellainen, että se voidaan kuvata toisen asteen yhtälöllä. Käytännössä tämä tarkoittaa sitä, että regressioanalyysia varten luodaan uusi muuttuja, joka saa arvoksi X-muuttujan arvon neliön (eli X^2). Kun nämä molemmat muuttujat lisätään regressioanalyysiin selittävinä muuttujina, voidaan esimerkin mukainen epälineaarinen yhteys analysoida regressioanalyysin avulla.
b) Poikkeavat havainnot eli outlier-tapaukset (outliers). Joskus yksittäisillä poikkeavilla havainnoilla voi olla suuri vaikutus regressioanalyysiin tuloksiin. Tällaisia havaintoja kutsutaan niiden englanninkielisen nimen mukaan outlier-tapauksiksi. Asia on havainnollistettu kuviossa 3. Kuvion oikeassa ylälaidassa oleva havainto on outlier-tapaus. Jos se poistetaan kuviosta, x- ja y-muuttujilla ei ole laisinkaan lineaarista riippuvuutta toisistaan.
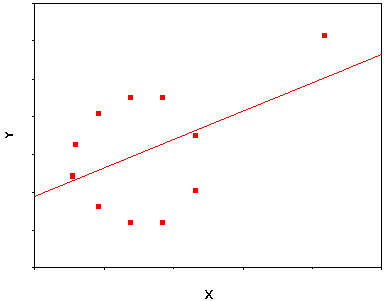
Kuvio 3. Esimerkki tilanteesta, jossa yksittäinen poikkeava havainto vääristää regressioanalyysin tuloksia.
Joskus poikkeavien havaintojen taustalla voi olla yksinkertaisesti koodausvirhe, joka voidaan helposti korjata. Useimmiten kyse on kuitenkin siitä, että jokin tai jotkut havainnot saavat todellisuudessa muista huomattavasti poikkeavia arvoja. Tällaisessa tilanteessa kannattaa pohtia, mikä tekijä aiheuttaa havainnon poikkeavuuden. Jos sille löytyy hyvä selitys joka voidaan mitata, voidaan tämä tekijä sisällyttää analyysiin uutena muuttujana, jolloin se ei enää vääristä analyysin tuloksia. Poikkeavien havaintojen löytämiseksi on kehitetty erilaisia tunnuslukuja (esimerkiksi Mahalanobisin ja Cookin etäisyysmittarit). Näistä luvuista ja niiden tulkinnasta löytyy tietoa lisätietoja-kohdassa suositelluista kirjoista (katso esimerkiksi Tabachnickin ja Fidellin kirja).
c) Multikollineaarisuus ja heteroskedastisuus. Regressioanalyysissa on aivan luonnollista, että selittävät muuttujat korreloivat keskenään. Joskus niiden keskinäinen korrelaatio voi kuitenkin olla niin suuri, että se aiheuttaa ongelmia regressioanalyysin tulosten tarkkuuden kannalta. Tällaista tilannetta kutsutaan multikollineaarisuudeksi. Yleensä multikollineaarisuusongelmia ei synny, jollei selittävien muuttujien välillä ole todella suuria riippuvuuksia (esimerkiksi korrelaatiokerroin yli 0,9). Ongelmana on, että kaikkia multikollineaarisuusongelmia ei voi havaita tarkastelemalla pelkästään selittävien muuttujien välisiä korrelaatiokertoimia. Tämän vuoksi on kehitetty erilaisia multikollineaarisuusmittareita, jotka ilmaisevat ongelman mahdollisen vakavuuden (esimerkiksi VIF-mittari).
Heteroskedastisuus viittaa tilanteeseen, jossa regressiomallin virhetermien hajonta vaihtelee suuresti ja systemaattisesti x-muuttujien arvojen muuttuessa. Kuviossa 4 havainnollistetaan heteroskedastisuutta. Kuvion y-akseli kuvaa selitettävän muuttujan arvoja ja x-akseli selittävän muuttujan arvoja. Kuvion esittämässä tilanteessa on kyse heteroskedastisuudesta siksi, että virhetermit vaihtelevat regressiosuoran ympärillä huomattavasti enemmän silloin kun x-muuttuja saa suuria arvoja.
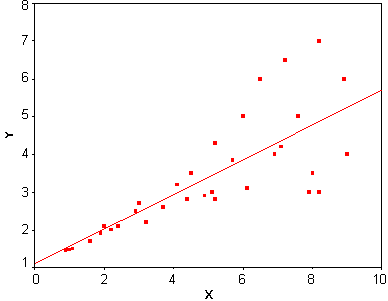
Kuvio 4. Esimerkki heteroskedastisuudesta.
Heteroskedastisuudella ei oikeastaan ole haitallisesta vaikutusta regressiokertoimien arvoon. Sen sijaan sillä voi olla vaikutusta niiden tilastolliseen merkitsevyyteen. Tämä voi johtaa esimerkiksi tilanteeseen, jossa tietty muuttuja ei näytä olevan tilastollisesti merkitsevä Y:n selittäjä vaikka se todellisuudessa sellainen onkin. Heteroskedastisuusongelmien havainnoimiseksi on kehitetty erilaisia testejä, joita ei kuitenkaan esitellä tässä yhteydessä. Yksinkertaisin tapa havainnoida mahdollisia heteroskedastisuusongelmia on tehdä aineistosta alustavan regressioanalyysin jälkeen kuvion 4 kaltaisia hajontakuvioita jokaisen selittävän muuttujan osalta. Jos hajontakuviot tai testit osoittavat, että aineistossa on heteroskedastisuutta, voidaan regressioanalyysin tulosten estimointiin käyttää sellaista menetelmää, joka pystyy ottamaan huomioon nämä ongelmat.
d) Havaintojen aikariippuvuus. Yksi regressioanalyysin perusolettamuksista on, että havaintojen virhetermit ovat toisistaan riippumattomia. Jos analysoitavana on aikasarja-aineisto (katso tutkimusasetelmat), tämä oletus ei useinkaan ole pätevä. Tämä johtuu siitä, että eri ajankohtina kerättyjen havaintojen virhetermit korreloivat keskenään. Jos analysoitavana on esimerkiksi työttömyyden taso jossain maassa eri vuosina, on tietyn vuoden työttömyystaso osittain riippuvainen edellisen vuoden tasosta. Jos tätä riippuvuutta ei oteta huomioon, regressioanalyysin tulokset vääristyvät. Havaintojen aikariippuvuuden korjaamiseksi on useita eri tapoja. Näistä kerrotaan esimerkiksi Ostromin kirjassa sekä ekonometrian oppikirjoissa (ks. lisätietoja-linkki).
