Ristiintaulukointi - SPSS-harjoitus 2

Jos olet ensimmäistä kertaa aloittamassa SPSS-harjoitusta MOTV-ympäristössä, on ennen varsinaisen harjoituksen tekemistä syytä tutustua opiskeluohjeisiin.

Tässä demonstraatiossa käytetään vuoden 2004 ISSP-tutkimuksen Suomen aineistoa, daF2039.
Havaintoaineiston hakemisesta SPSS-ohjelmaan on erilliset ohjeet.

Kolmiulotteinen ristiintaulukko

» daF2039-aineisto | Harjoitusaineistot

Seuraavaksi tehtävän kolmiulotteisen ristiintaulukon avulla voit verrata vakituisen kumppanin kanssa elävien ja muiden naisten sekä miesten arvioita siitä, voiko ihmisiin luottaa.

Ennen varsinaista harjoitustehtävää voit omatoimisesti tutkia perinteistä ristiintaulukointia sukupuolen ja ihmisiin luottamisen välillä. Tarvittavat muuttujat ja näiden muunnokset on esitelty myöhemmin.

Ristiintaulukointi ja tähän liittyvä khiin neliötesti (-testi) antaa tuloksen, jonka mukaan naisten ja miesten luottamus muihin ihmisiin eroaa toisistaan tilastollisesti melkein merkitsevästi (p=0,04). Naiset näyttäisivät olevan miehiä hieman useammin sitä mieltä, että toisiin ihmisiin voi luottaa.

Seuraavaksi yritetään selittää tarkasteltavia näkemyseroja vielä paremmin uuden ryhmittelevän muuttujan avulla. Siirrytään tarkastelemaan luottamuksen määrää siitä riippuen, asuuko vastaaja vakituisen kumppanin kanssa vai ei.

Tarvittavat muuttujat ovat:

k1 Sukupuoli
k4 Asutteko nykyisin yhdessä puolison tai vakituisen elämänkumppanin kanssa ja
k42 Sanoisitteko, että ihmisiin voi yleensä luottaa vai että yleensä kannattaa pitää varansa muiden ihmisten kanssa

Ristiintaulukointia varten luokitellaan kysymys 42 uudelleen kahteen luokkaan (SPSS valikosta Transform - Recode into Different Variables), ja annetaan uudelle muuttujalle nimeksi esim. k42u. Labeliin voidaan samalla kirjata kysymysteksti uudestaan.

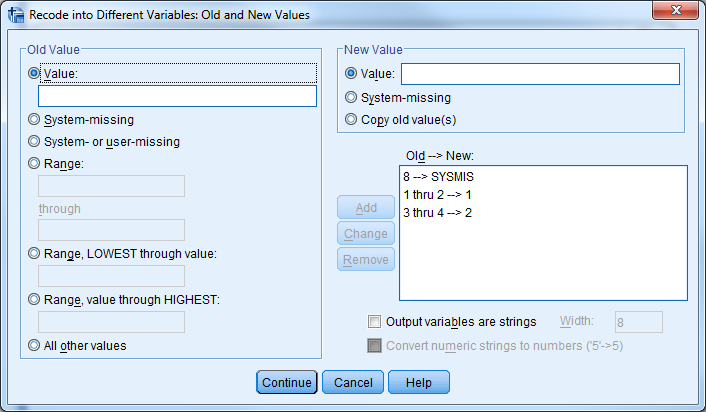
Ne, joiden mielestä ihmisiin voi lähes aina tai useimmiten luottaa (vaihtoehdot 1 ja 2) laitetaan samaan luokkaan, ja ne, joiden mielestä muiden ihmisten kanssa kannattaa useimmiten tai lähes aina pitää varansa (vaihtoehdot 3 ja 4), toiseen. En osaa sanoa -vaihtoehto (8) koodataan puuttuvaksi. Merkitään uusia luokkia numeroin 1 ja 2, ja käydään myös antamalla niille otsikot Value labels -sarakkeessa. Tämä helpottaa tulosten tarkastelua jatkossa.

Ristiintaulukoinnin ikkuna avautuu komennolla Analyze - Descriptive Statistics - Crosstabs...

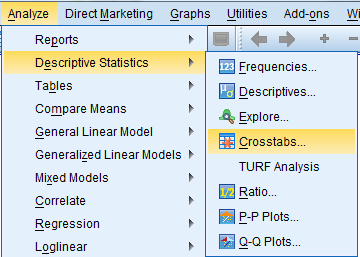
Crosstabs-taulun avauduttua klikkaa ensimmäiseksi Reset-painiketta, jolloin Crosstabs-toiminnon mahdolliset aikaisemmat määritykset häviävät.

Kolmiulotteista ristiintaulukkoa varten tehtävät määritykset eroavat hieman edellisestä esimerkistä. Rivi- ja sarakemuuttujien määrittämisen lisäksi tulee määritellä ne luokat, joissa rivi- ja sarakemuuttujien yhteyksiä tutkitaan. Tämä tehdään Layer-valikon avulla.

Lisäksi voidaan tehdä samoja testejä ja solumäärityksiä kuin kaksiulotteisillekin ristiintaulukoille (ks. Harjoitus 1).

Kolmiulotteisessa ristiintaulukossa rivi- ja sarakemuuttujat kannattaa järjestää hieman eri tavalla kuin tavallisessa ristiintaulukossa, sillä SPSS järjestää automaattisesti Layer-valikkoon valittavan muuttujan riveille. Molemmat syymuuttujat kannattaa esittää samalla puolella taulukkoa, joten toinen myös selittävä muuttuja kannattaa valita rivimuuttujaksi.

Mihin laatikoihin laittaisit käytettävät kolme muuttujaa?

Valitse muuttujaluettelosta hiirellä klikkaamalla sukupuolimuuttuja

k1 Sukupuoli

ja siirrä se nuolen avulla Row(s): -laatikkoon.

Etsi muuttujaluettelon lopusta muuttujasta k42 muodostettu uusi muuttuja k42u ja siirrä se Column(s): -laatikkoon.

Etsi vielä kumppanin kanssa asumista kuvaava k4, ja siirrä se Layer 1 of 1 -laatikkoon.

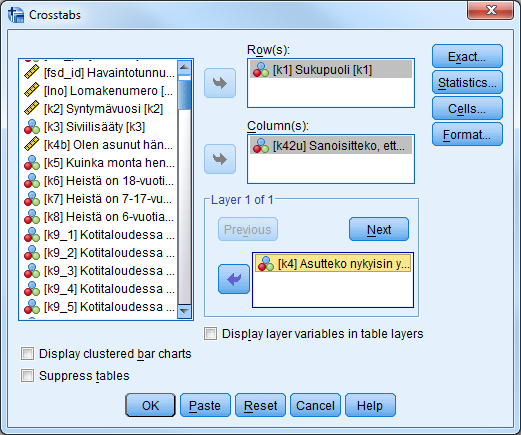
Kuten kahteen ensimmäiseenkin laatikkoon, myös Layer-laatikkoon voidaan siirtää useita muuttujia, jolloin ohjelma muodostaa kaikki mahdolliset annettujen muuttujien väliset ristiintaulukkokombinaatiot.

Layer-otsikon alta voi myös klikata Next -kohtaa, jolloin pääsee määrittämään uuden/uusia rivimuuttujia, jotka ryhmittelevät havaintoja. Tämän käyttöä ei kuitenkaan suositella, sillä jo kolmiulotteinen ristiintaulukko on usein raskas tulkittava ja solufrekvenssit saattavat jäädä liian alhaisiksi.

Määrittele ristiintaulukkoon riviprosentit vielä ennen OK:ta ja khii toiseen testin määritystä:

Klikkaa hiirellä Cells... -painiketta, jolloin ristiintaulukon soluihin viittaavat määritykset avautuvat:

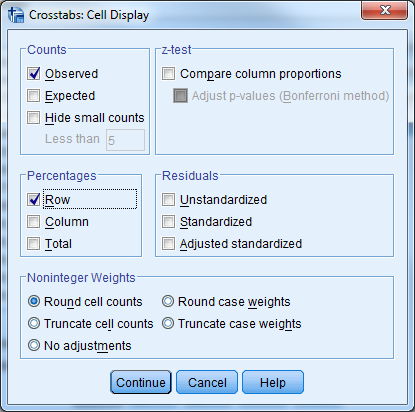
Kuten aikaisemmassa harjoituksessa, valitaan näytettäväksi havaitut solufrekvenssit (Counts - Observed) sekä prosentit syymuuttujien eli sukupuolen ja kumppanin kanssa yhdessä asumisen mukaan.

Percentages - laatikosta siis valitaan tällä kertaa Row.

Muut mahdolliset solumääritykset on esitelty edellisessä tehtävässä (Harjoitus 1).

Hyväksy valitsemasi solumääritykset Continue-painikkeella.

Siirry seuraavaksi määrittämään khiin neliön testi ( -testi ) valitsemalla Statistics... -painike.

Valitse Crosstabs: Statistics -näkymän vasemmasta yläreunasta Chi-square.

Siirry Continue -painikkeella takaisin Crosstabs-tauluun, ja valitse lopuksi OK.

Tutki ensin ristiintaulukkoa. Saitko samanlaisen?

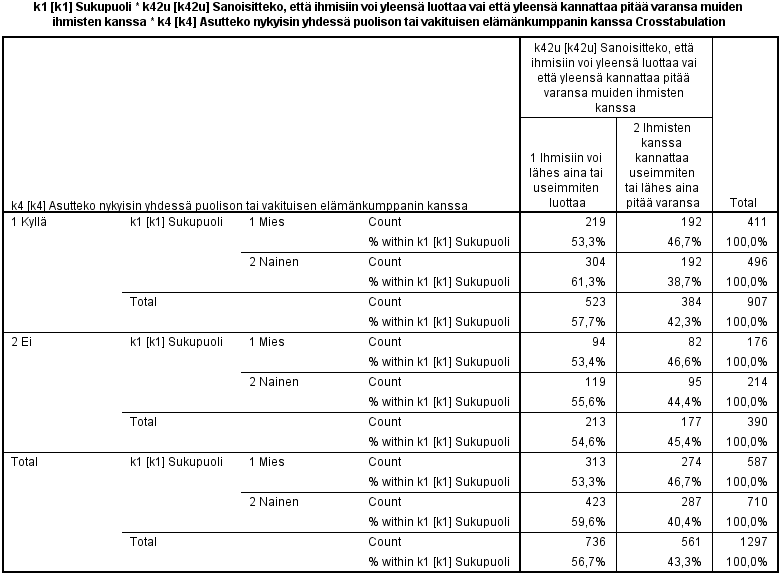
Elleivät lukuarvot ole samoja, tarkista, onko sarakemuuttuja oikein määritelty muuttujan k42 pohjalta. Mieti myös, oletko käyttänyt edellä esim. Select Cases tai Split file -toimintoa, joka olisi jäänyt päälle.

Solujen koot ovat todennäköisesti erit omassa taulukossasi, sillä näitä muokattiin malliesimerkkiä tehdessä tilan säästämiseksi.

Huomaa, että käsittelyssä on kaksi itsenäistä ristiintaulukkoa, jotka on saatu jakamalla aineisto sen mukaan, asuuko vastaaja yhdessä kumppanin kanssa. Tämän tarkastelun pohjalta ei siis voi tarkastella kaikkien vastaajien luottamusta muihin ihmisiin.

Muuten taulukon tulkinta on hyvin samankaltaista kuin normaalin ristiintaulukon. Taulukosta voi tehdä esimerkiksi seuraavat päätelmät:

Reunajakaumat:

• Aineistossa 907 vastaajaa asuu ja 390 ei asu yhdessä vakituisen elämänkumppanin kanssa.
• Kaikkien vastaajien sukupuolijakaumaa ei voi lukea suoraan taulukosta; naisten ja miesten lukumäärät voi kylläkin laskea Total-sarakkeen frekvenssien avulla (esim. miehiä on 411 + 176 = 587).
• Yhdessä kumppanin kanssa asuvista 523 (= 57,7 %) on sitä mieltä, että ihmisiin voi lähes aina tai useimmiten luottaa, ja vastaava lukumäärä ilman kumppania elävien kohdalla on 213 (= 54,6 %).

Ehdolliset jakaumat eli naisten ja miesten jakaumat:

• Vakituisen kumppanin kanssa asuvista naisista 61,3 % katsoo, että ihmisiin voi useimmiten luottaa, kun taas vastaavassa elämäntilanteessa olevista miehistä 53,3 % on tätä mieltä.
• Ilman vakituista asuinkumppania elävien kesken erot sukupuolten välillä eivät ole yhtä suuret; tässä joukossa naisista 55,6 % ja miehistä 53,4 % on sitä mieltä, että ihmisiin voi useimmiten luottaa.

Kuten harjoituksen alussa mainittiin, tiedetään jo, että naisten mielestä ihmisiin voi luottaa useammin kuin miesten mielestä. Tulkinnan kannalta mielenkiinnon kohteena ovat nyt "uloimman tason" eli tässä asumis-muuttujan osoittamat erot ehdollisiin jakaumiin.

Tiivistetty tulkinta ristiintaulukosta: Ilman kumppania elävien kesken luottamus ihmisiin on yhtä suurta naisten ja miesten kesken. Elämänkumppanin kanssa asuminen taas lisää naisten, muttei miesten, yleistä luottamusta ihmisiin. Mikä voisi selittää tätä eroa?

Kun olet perehtynyt ristiintaulukkoon, siirry khiin neliön testituloksiin ( -testiin ).

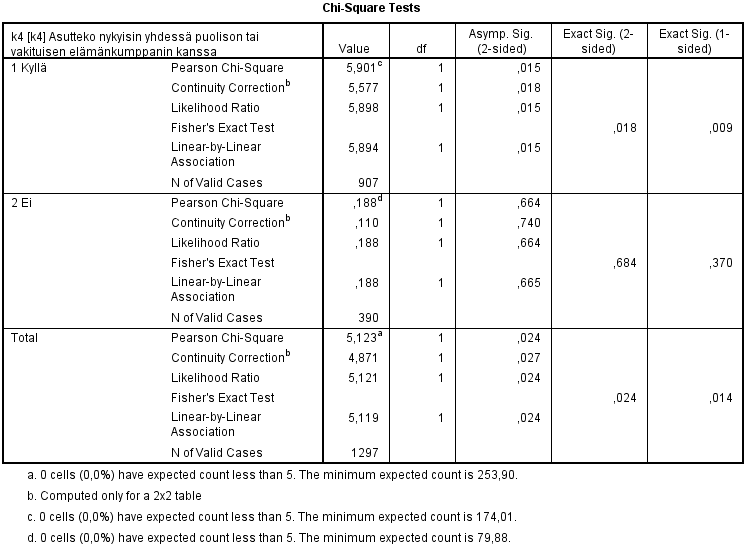
Kuten aina khiin neliön testin (-testin) kohdalla, tulee ensimmäisenä tarkistaa, että testin oletukset ovat kunnossa. Erityisesti moniluokkaisten ristiintaulukoiden kohdalla odotetut solufrekvenssit jäävät helposti liian pieniksi.

Ovatko -testin oletukset kunnossa?

Kummassakaan taulukossa yhdenkään solun odotettu frekvenssi ei ole alle viiden (sallittu maksimi 20 % kaikista soluista), ja myös pienimmät odotetut frekvenssit ovat monikymmenkertaisesti yli sallitun minimiarvon 1. Testin esittämä tulos on siis validi.

Pearsonin khiin neliön testiin (-testiin) liittyvä p-arvo on ylemmässä ristiintaulukossa 0,015, ja alemmassa 0,664. Tämä tukee jo ristiintaulukoinnin perusteella tehtyä päätelmää siitä, että yhdessä kumppaninsa kanssa elävien naisten ja miesten välillä on eroja sen suhteen, voiko heidän mielestään ihmisiin yleensä luottaa vai ei. Testin tulos kertoo, että nämä erot ovat tilastollisesti merkitseviä.

Myös ilman kumppania elävien naisten ja miesten vastauksissa oli pieniä eroja, mutta jos eroja pidettäisiin merkitsevinä, olisi kuitenkin 66,4 % (=100*0,664) todennäköisyys, että päätelmä olisi väärä. Tämä ylittää reilusti minimiriskitasona pidetyn 5 %.

Nyt voit tehdä toisenlaisen, itse valitsemasi ristiintaulukon ja kerrata oppimaasi:

Valitse Analyze - Descriptive Statistics - Crosstabs... tai voit käyttää Dialog Recall -pikakuvaketta klikkaamalla sitä kerran ja valitsemalla ylimmäisenä olevan Crosstabs-toiminnon.

Crosstabs-toiminnon avauduttua voit tyhjentää kaikki aiemmin annetut määritykset painamalla Reset.